A Bell-egyenlőtlenség
Korreláció és információáramlás
Ha két eseménysor között valamilyen összefüggés (korreláció) állapítható meg, amelynek az okát fel akarjuk deríteni, két alapvető magyarázat-típussal próbálkozhatunk. Vagy azt tesszük fel, hogy az egyik (mondjuk A) eseménysor oka a másiknak (B-nek), vagy mindkét eseménysort egy harmadikra (C-re), mint közös okra igyekszünk visszavezetni. Természetesen előfordulhat ennek a két alapvető determinációs típusnak különféle arányú kombinációja is, azonban az egyszerűség kedvéért a továbbiakban a tiszta esetekre szorítkozunk. A korreláció első típusát, amelynél az A a B oka, egyenes irányú korrelációnak, a másodikat közös ok típusú korrelációnak, vagy kauzális villának fogjuk nevezni (1. ábra). A kauzális villában természetesen az A és a C, illetve a B és a C közötti korreláció egyenes irányú, csak az A és a B közötti összefüggés közös ok típusú.
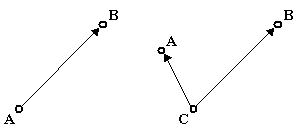
1. ábra – Egyenes irányú és közös ok típusú korrelációk
A korreláció típusának a megállapításában az információáramlás irányának van meghatározó szerepe. Az információ mindig az okból kiindulva áramlik az okozat felé, ezért az egyenes irányú korrelációnál az A-tól a B felé, a közös ok típusú korrelációnál pedig C-től az A és a B felé terjed.
Noha eddigi megállapításaink meglehetősen nyilvánvalóak, illusztráljuk őket mégis egy példával. Ha azt találjuk, hogy egy este két különböző lakásban a tévékészüléken ugyanaz a műsor fut, ez két olyan eseménysor, amelyek között szoros korreláció áll fenn. A két eseménysor összefüggése nem egyenes irányú, mert ha az egyik készüléket kikapcsoljuk, a műsor a másikon változatlanul pereg tovább. A műsorok azonosságát tehát nem a készülékek között haladó információ biztosítja, ezért a korreláció nem lehet más, mint közös ok típusú. A közös ok a tévé stúdióban folyó “eseménysorozat”, amelyről az információ a kamerákon és az adóállomáson keresztül végül elektromágneses hullámok formájában fénysebességgel terjed a készülékek felé.
De mi van akkor, ha aznap este a tévé egészen más műsort sugároz, mint amit a két kiszemelt készülék képernyőjén látunk? Nyilvánvalóan nem lehet puszta véletlen, hogy másfél órán keresztül ugyanazok a képsorok (jelkombinációk) jelennek meg mindkettőn. Ez a helyzet például akkor, ha mindkét készülék videóról jár, amelybe véletlenül vagy szándékosan ugyanazt a filmet tartalmazó műsorkazettát tették be. Ebben az esetben is kauzális villával állunk szemben. A közös ok a magnószalagokon őrzött film felvételéhez kapcsolódó eseménysor, amelyről az információ a film előhívását, átjátszását, a magnószalagok terjesztését magában foglaló bonyolult rendszeren keresztül jutott el a képernyőkre.
Az alább következő meggondolásokban a hangsúlyt mindig az eseménysorok közötti determinációs típus vizsgálatára fektetjük, a korrelációt meghatározó információ-áramlás közegének a természetét másodlagosnak tekintjük. Ez a közeg még egyetlen információs láncon belül is a legkülönbözőbb elemekből állhat, amelyeket esetenként még felsorolni is nehéz. Példánkban információhordozó közegként megtaláljuk egyebek között az elektromágneses teret és a magnószalagok anyagát. A fizikai problémák zöme éppen ehhez a közeghez fűződik, mégis tekintsünk el most tőlük, és fordítsuk figyelmünket arra az érdekes körülményre, hogy az információhordozó közeg rendkívüli sokrétűségével szemben a determinációs alaptípusok száma kicsi, mindössze kettő. Mi több, míg a közegek tulajdonságait csak részletes, fáradságos vizsgálattal lehet fokozatosan felderíteni, addig a determinációs típusok a felfogásunkban mintegy eleve adottak. Így például ha az egyenes irányú korreláció lehetőségét kísérletileg kizárjuk, mint ahogy ez a tévé készülékekkel történt, már tudjuk, hogy a korreláció csakis közös ok típusú lehet és teljes figyelmünket ennek a közös oknak a megtalálására fordíthatjuk. Vajon nem esünk-e itt áldozatul valamiféle optikai csalódásnak? Nem lehetséges-e, hogy a természetben a determinációs formák gazdagabbak, mint ahogy elképzeljük és bizonyos formák csak azért nem épültek be a szemléletünkbe, mert érzékszerveink a fizikai jelenségeknek csak korlátozott körére reagálnak?
Az elmúlt húsz év vizsgálatai arra mutatnak, hogy valószínűleg tényleg léteznek olyan összefüggő eseménysorok, amelyek determinációs típusa nem lehet sem egyenes irányú, sem közös ok típusú. Annak ellenére, hogy e két típuson kívül semmilyen más determinációs formát sem vagyunk képesek elgondolni, elképzelhetők olyan kísérletek, amelyekben korrelációt tapasztalunk és ugyanakkor mindkét determinációs típus kizárható. Már azt is jelentős lépésként könyvelhetjük el, hogy pusztán logikai úton, képzeletben sikerül ilyen kísérletet konstruálni. Valójában azonban lényegesen többről van szó – a kvantumfizikai jelenségek segítségével meg is valósíthatók olyan összefüggő makroszkopikus eseménysorok, amelyek a két determinációs típus egyikébe sem sorolhatók.
A következő fejezet az elképzelt kísérlet leírását tartalmazza. Ez egyrészt a jobb érthetőséget szolgálja, másrészt nyilvánvalóvá teszi, hogy a két determinációs típus elégtelenségének a feltárásához egyáltalán nincs szükség a kvantumelméletre. A pusztán logikai lehetőségek realizálása a természetben persze más kérdés. A reális kísérleteket a harmadik fejezetben tárgyaljuk.
Egy képzeletbeli kísérlet
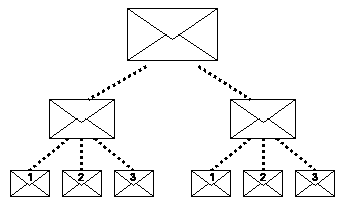
A kísérletben három személy vesz részt, akiket A-nak, B-nek és C-nek fogunk nevezni. Mindegyik egy-egy külön szobában foglal helyet: a középső szobában C, a baloldaliban A, a jobboldaliban B (2. ábra). C asztalán egy halom teljesen egyforma lezárt nagy alakú borítékot látunk. Mindegyik nagy alakú boríték két tökéletesen egyforma külsejű lezárt közepes borítékot tartalmaz. Végül mindegyik közepes borítékban három kisalakú boríték van, amelyek közül az egyik az 1., a másik a 2., a harmadik a 3. számot viseli (3. ábra). Ha akármelyik kis alakú borítékot felnyitjuk egy kék vagy egy piros korongot találunk benne. Ezeknek a színeknek az eloszlása a borítékokban képezi a “kísérleti vizsgálat” tárgyát.
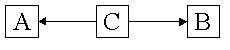
2. ábra – A kísérlet elrendezése
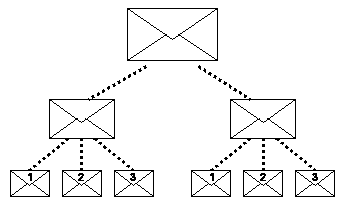
3. ábra – A kísérlet menete
A szabályok azonban nem engedik meg, hogy a borítékokat csak úgy vaktában, minden korlátozás nélkül nyitogathassuk fel, hanem csak a következő eljárást teszik lehetővé: A középső szobában C találomra kiválaszt egy nagy borítékot, felnyitja és a két közepes boríték közül az egyiket átküldi A-nak a baloldali, a másikat pedig B-nek a jobboldali szobába. Itt A és B felbontja ezeket a borítékokat, a három számozott boríték közül kiválasztanak találomra (mondjuk egymástól független kockadobás alapján) egyet és a másik kettőt még lezárt formában azonnal megsemmisítik. A kiválasztott borítékot mindketten felnyitják és megnézik, milyen színű korong van benne. A boríték számát és a korong színét gondosan feljegyzik. Egy idő múlva a középső szobában C megint kiválaszt egy nagy borítékot és az egész eljárás ismétlődik.
Miután egy csomó borítékot ilyen furcsa módon átvizsgáltak, a résztvevők a kísérletet befejezettnek nyilvánítják, összejönnek az egyik szobában és A és B listáját egymás mellé helyezik. Ennek a kétoszlopos listának az első sorait látjuk az 1. táblázatban. A szám a boríték sorszámát, K és P a korong színét jelzi. A “valóságos” lista természetesen sokkal hosszabb és első ránézésre semmilyen szabályszerűséget sem árul el. Tegyük fel azonban, hogy a türelmes tanulmányozás mégis fölfed egy egyszerű szabályosságot, amely kivétel nélkül mindig teljesül: azokban a sorokban, amelyekben a boríték száma mindkét oszlopban azonos, a két szín mindig különböző (a lista elején ilyen a harmadik és az ötödik sor).
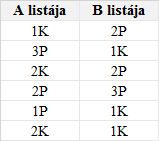
1. táblázat
A színek eloszlása a borítékokban tehát nem teljesen véletlenszerű: egy nagy borítékon belül az azonos számozású kis borítékok mindig különböző színű korongot tartalmaznak.
A kísérlet folyamán A és B gondosan jegyezte a borítékok sorszámát és a korongok színét. A feljegyzések aktusa két eseménysort alkot. A listák utólagos egymás mellé helyezése alapján látjuk, hogy a két eseménysor között határozottan van valamilyen összefüggés, hiszen valahányszor mind A, mind B véletlenül ugyanazt a sorszámú kis borítékot nyitotta ki, mindig határozottan különböző színt jegyeztek fel. Vajon milyen lehet a korreláció típusa a két eseménysor között?
Első pillantásra a válasz nyilvánvalónak látszik – csak közös ok típusú korrelációról lehet szó. Az az információ, amely A és B feljegyzéseit meghatározta, csakis a közepes borítékban juthatott el a középső szobából a két szélső szobába. Egyszerűbben szólva, a nagy borítékok ismeretlen előkészítői gondosan ellenkező színű korongot helyeztek el minden nagy boríték két azonos sorszámú kis borítékjában és az erről szóló információt a korongok festékanyaga közvetítette A és B felé.
Bármennyire meggyőző is ez a magyarázat, a kísérletezők arra az elhatározásra jutnak, hogy a szigorú szabályok adta lehetőségeken belül más, független módon is megpróbálnak meggyőződni arról, valóban terjed-e információ a borítékokban. Ez a kétely első hallásra oktalannak és túlzottnak hat, mégis – mint a továbbiakból remélhetően kiderül, – éppen ennek a kérdésnek a feltevése bizonyul majd gondolatmenetünk legfontosabb láncszemének. Vizsgáljuk meg hát türelmesen, eloszlatható-e valamilyen módon ez az aggály.
Mivel az információt a korongok színe hordozza, arról kell igazából meggyőződni, hogy a korongok akkor is színesek, amikor még a kísérletezők számára láthatatlanul a borítékban lapulnak. Ha ugyanis például a korongok csak a boríték felnyitásának pillanatában – mondjuk a levegővel való érintkezés hatására, – veszik fel a kék vagy a piros színt, akkor megtörténhet, hogy a színüket nem a borítékban közvetített információ határozza meg. Ilyen esetben a korreláció magyarázatául szolgáló információ-áramlást másutt kell keresnünk1. De ki lehet-e olvasni egy olyan táblázat adataiból, amely a korongoknak csak a borítékok felnyitása után látható színét tartalmazza azt, hogy volt-e határozott színük a borítékok felnyitása előtt? Bármilyen meglepő, az 1. táblázat adatai tartalmaznak erre vonatkozó utalást is.
A táblázatban összesen 36 féle sortípus fordul elő. Mindegyik oszlopban a két szín és a három sorszám 2 · 3 = 6 lehetőséget eredményez, ami a két oszlopra vonatkozóan 62 = 36 kombináció. Ebből 3 · 22 = 12 olyan eset van, amikor a borítékok sorszáma mindkét oszlopban azonos, de ebből a 12-ből a táblázatban valójában csak 6 fordul elő: azok, amelyekben a színek különböznek egymástól. Összesen tehát 24 + 6 = 30 különböző sort találunk a táblázatban. Ha az oszlopok sorrendjétől eltekintünk – vagyis pl. az (1P, 2K) és a (2K, 1P) típusú sorokat azonos csoportba soroljuk, – akkor csak a következő 15 különböző sortípus marad meg: (1P, 1K), (1P, 3P), (2P, 2K), (3P, 3K), (1P, 2P), (1P, 2K), (1P, 3K), (2P, 3P), (2P, 1K), (2P, 3K), (3P, 1K), (3P, 2K), (1K, 2K), (1K, 3K), (2K, 3K).
Jelöljük N(1P, 1K)-val azoknak a soroknak a számát, amelyek az egyik oszlopban 1P-t, a másikban 1K-t tartalmaznak és definiáljuk hasonló módon az N(2P, 2K)-t, N(3P, 3K)-t egészen N(2K, 3K)-ig. Ha a táblázat nagyon sok sort tartalmaz, akkor a különböző lehetőségek relatív gyakoriságából empirikusan meghatározhatjuk az egyes kombinációk előfordulási valószínűségét. Így pl. annak valószínűsége, hogy az egyik oszlopban 1P, a másikban 2P szerepeljen, a következő:
p(1P, 2P) = N(1P, 2P) / N
ahol N a sorok száma a táblázatban. Ilyen módon összesen 15 különböző lehetőség valószínűségét olvashatjuk le, amihez hozzávehetjük a következő 6 ismert valószínűséget:
| p(1P, 2P) = p(2P, 2P) = p(3P, 3P) = | [1] |
| = p(1K, 2K) = p(2K, 2K) = p(3K, 3K) = 0 |
Ez utóbbi egyenlőségek fejezik ki azt a nagyon szoros korrelációt, amely a két szélső szobában lezajló eseménysorok között a táblázat adatai alapján fennáll. Ha ezeket az egyenlőségeket még kiegészítjük azzal a feltevéssel, hogy az egész kísérlet folyamán minden egyes korong végig meghatározott színnel rendelkezett, akkor a 15 + 6 = 21 darab empirikus valószínűség között szükségképpen fenn kell állniok bizonyos korlátozó egyenlőtlenségeknek, amelyeket felfedezőjükről Bell-egyenlőtlenségeknek nevezünk2.
Tételezzük fel tehát, hogy minden korong határozottan kék, vagy piros, ahogy azt a józan ész alapján elvárjuk. Anélkül, hogy a játékszabályok súlyos megsértésével az összes kis borítékot egyszerre felbontanánk, könnyen meggyőződhetünk arról, hogy mindössze 4 különböző típusú nagy boríték fordulhat elő a C kísérletező asztalán. Először is, ha valamelyik nagy boríték egyik közepes borítékjában az 1. kis borítékban mondjuk kék, a 2.-ben piros, a 3.-ban megint kék korong van, akkor (1) következtében bizonyos, hogy ugyanezen nagy boríték másik közepes borítékjában az 1. kis boríték piros, a 2. kék, a 3. piros korongot tartalmaz. Ez a meggondolás természetesen bármely színkombinációra érvényes és azt mutatja, hogy minden nagy borítékban elég lenne csak az egyik közepes boríték tartalmát megvizsgálni ahhoz, hogy eldöntsük, milyen típusú (azaz mit tartalmaz) az egész nagy boríték. Egy közepes boríték viszont 23 = 8 különböző eloszlásban tartalmazhatja a korongokat, ezért minden nagy boríték a 2. táblázatban feltüntetett 4 típus valamelyikébe sorolható.

2. táblázat
Ha a szabályok megengednék, akkor a relatív gyakoriság leszámlálásával megállapíthatnánk, mekkorák az egyes típusok wi (i = a, b, c, d) előfordulási valószínűségei. De annyit a szabályok megsértése nélkül is megtehetünk, hogy pl. a p(1P, 2P) valószínűséget az ismeretlen wi-ken keresztül kifejezzük. Nyilvánvaló, hogy csak azok a nagy borítékok vezethetnek 1P, 2P vagy 2P, 1P típusú bejegyzésre az 1. táblázatban, amelyek c., vagy d. típusúak. Annak valószínűsége, hogy egy nagy boríték ezen típusok valamelyikébe tartozzon (wc + wd)-vel egyenlő. Annak valószínűsége pedig, hogy az a kísérletező, akihez az (1P, 2K, 3K), vagy az (1P, 2K, 3P) típusú boríték került éppen a 2. kis borítékot nyissa fel (1/3) ∙ 2 = 1/9-el egyenlő, mert mindkét kísérletező független kockadobással állapítja meg a felnyitandó boríték sorszámát. Így
| p(1P, 2P) = 1/9 ∙ (wc + wd) | [2] |
A 15 darab p(1P, 1K), p(1P, 3P),… p(2K, 3K) valószínűségét mind felírhatjuk hasonlóan egyszerű módon a négy wa, wb, wc, wd-n keresztül, amelyek közül a wa + wb + wc + wd = 1 reláció miatt valójában csak három független. A p valószínűségek között ezért nagyon sok összefüggésnek kell fennállnia. A kísérletekkel való összevetés szempontjából a már említett Bell-egyenlőtlenségeknek van fontos szerepe, amelyek a w valószínűségek pozitivitását fejezik ki a p-k nyelvén, mert ilyen egyenlőtlenségek akkor is levezethetők, amikor a korreláció gyengébb és a viszonyok bonyolultabbak, mint képzeletbeli kísérletünkben.
Egy tipikus Bell-egyenlőtlenség például a következő:
| p(1P, 2P) + p(2P, 3P) ≥ p(1P, 3P) | [3] |
Ennek a relációnak az igazolása nagyon egyszerű. A 2. egyenletre vezető gondolatmenethez hasonló okoskodással azt találjuk, hogy
p(2P, 3P) = 1/9 ∙ (wb + wd);
p(1P, 3P) = 1/9 ∙ (wb + wc)
Ezeket és p(1P, 2P) 2. kifejezését, a 3. kifejezésbe írva egyszerűsítés után a wd ≥ 0 egyenlőtlenségre jutunk, amelynek valóban teljesülnie kell, hiszen wd, a d. típusú nagy boríték előfordulási valószínűsége nem lehet negatív szám.
A 3-as Bell-egyenlőtlenség két alkotóelemet egyesít magában: azt a tapasztalati tényt, hogy minden nagy borítékban a két azonos számozású kis boríték mindig különböző színű korongot tartalmaz, valamint azt a feltevést, hogy a korongok színe, ahogyan azt a kis boríték felnyitása után észleljük, már a borítékba való behelyezés pillanatában eldőlt. Ha az 1. táblázatból számítható p valószínűségek nem elégítik ki a Bell-egyenlőtlenséget, e két összetevő közül valamelyiknek érvénytelennek kell lennie. Az elsőt a tapasztalat közvetlenül igazolja, a második azonban csak feltevés és így csak ez utóbbi sérülhet. De akkor a tapasztalatilag észlelt korreláció nem közös ok típusú, mert a korrelációt meghatározó információ nem a borítékok közvetítésével terjed C-től A és B felé. Az A-tól közvetlenül B felé vagy fordítva terjedő információ-áramláson alapuló egyenes irányú korrelációt is kizárhatjuk, hiszen a kísérlet megengedi, hogy A-t és B-t a legszigorúbban izoláljuk egymástól és arról is gondoskodhatunk, hogy a borítékokat mindig pontosan azonos pillanatban nyissák fel. Ezért a Bell-egyenlőtlenség sérülésekor a két alapvető determinációs típus, amelyet a szemléletünk megenged, elégtelen a megfigyelhető korreláció értelmezéséhez.
Természetesen ha ezt a naiv kísérletet a borítékokkal tényleg elvégeznénk és valóban azt tapasztalnánk, hogy az azonos számozású kis borítékok mindig különböző színű korongot tartalmaznak, akkor a Bell-egyenlőtlenség bizonyosan fennállna és a korreláció közös ok típusú volna. Ennek így kell lennie, hiszen az a játékszabályunk, hogy az összes borítékot nem szabad egyszerre felnyitni, puszta megállapodás, amit bármelyik pillanatban felfüggeszthetünk. Ha ezt valóban megtesszük, a wi valószínűségeket a p-ktől függetlenül közvetlenül is meghatározhatjuk és ezért nem kaphatunk rájuk negatív értékeket. Ez pedig elegendő a Bell-egyenlőtlenség teljesüléséhez.
A képzeletbeli borítékos kísérletnek azonban lehet olyan analogonja, amelyben a borítékok egyidejű felnyitásának megfelelő lépést valamilyen áthághatatlan természeti törvény tiltja meg. Ilyen helyzet áll elő a kvantumelméletben, ahol az i.-k boríték felnyitásával egy Ai fizikai mennyiség mérése állítható párhuzamba. Ha az A1, A2, A3 fizikai mennyiségek operátorai nem kommutálnak egymással, akkor egyszerre csak az egyik mennyiséget tudjuk megmérni – ez a törvény felel meg annak a tilalomnak, hogy mindig csak az egyik kis borítékot szabad felbontanunk. Ilyen körülmények között az előző bekezdés gondolatmenetét már nem használhatjuk fel a Bell-egyenlőtlenség teljesülésének a demonstrálására. Sőt, ha a kvantumelmélet segítségével a megfigyelhető p valószínűségeket kiszámítjuk azt találjuk, hogy bizonyos körülmények között ezek az egyenlőtlenségek nem teljesülnek, és ezekben az esetekben egymástól tetszőlegesen nagy távolságban történő eseménysorok korreláltak lehetnek anélkül, hogy felfedezhető volna olyan információ-áramlás, amely a korreláció magyarázatául szolgálhatna.
A Bell-egyenlőtlenség sérülése spinkorrelációs kísérletekben
Az előző fejezetben ismertetett képzeletbeli kísérlet minden olyan vonását, amely a korrelációk szempontjából lényeges, tartalmazza az a reálisan is elvégezhető kísérlet, amelynek a leírására most térünk át. Képzeljük el, hogy a középső szobában a C kísérletező bizonyos előre meghatározott időpontokban előállít egy neutronból és egy protonból álló rendszert, amelyben a két részecske teljes spinje zérus. A magfizikából ismeretes, hogy egy ilyen állapotban a magerő nem elégséges ahhoz, hogy a két részecskét összetartsa (a deuteron spinje 1-el egyenlő), ezért a rendszer azonnal szétesik, a neutron és a proton egymással ellentétes irányban, azonos sebességgel szétrepül. Az esetek bizonyos hányadában mozgásirányuk olyan, hogy egyikük a jobboldali, másikuk a baloldali laboratóriumon halad keresztül, ahol az A és a B kísérletező a spinvetületükre vonatkozó mérést végezhet el rajtuk.
A kezdőpillanatban a széteső rendszer teljes spinje zérus (S = 0), és a kvantumelmélet szerint ez a tulajdonság megmarad mindaddig, amíg a részecskék beavatkozástól mentesen szabadon mozognak. Azt, hogy a spin valóban zérus, a szétbomlás után is lehet ellenőrizni a jobboldali és a baloldali laboratóriumban végezhető alkalmas mérés segítségével. Ehhez az szükséges, hogy mindkét laboratóriumban megmérjék az áthaladó részecske spinvetületét ugyanarra az n irányra. Ha a teljes spin zérus, akkor az egyik részecske spinvetülete +ℏ/2, a másiké -ℏ/2, akármilyen legyen is a közös n mérési irány.
A spinvetület mérése Stern-Gerlach kísérlet segítségével történik, amelyben a részecskéket speciálisan kialakított mágnespofák között engedik át. A mágnespofák helyzete kijelöli azt az n irányt, amely mentén a mágneses mező változása a leggyorsabb. A berendezésen áthaladó részecskék egy része a +n, másik része a –n irányba térül el aszerint, hogy spinvetületük az n irányra +ℏ/2-vel vagy -ℏ/2-vel egyenlő. Ezzel az eljárással minden egyes részecskéről megállapítható, milyen előjelű a spinvetülete a berendezés által megszabott n irányban.
Az előző fejezetben tárgyalt kísérlet spinekkel elvégezhető analogonja a következő: A középső laboratóriumból a C kísérletező meghatározott időpontokban egy-egy S = 0 állapotú neutron-proton párt indít el. Mielőtt még a részecskék a két szélső laboratóriumba érnének A és B a saját Stern-Gerlach berendezését olyan helyzetbe állítja be, hogy azok három előre megállapított n1, n2, n3 irány valamelyikére vetett spinvetület előjelét mérjék. Az irányt minketten független kockadobás alapján állapítják meg. Feltesszük, hogy a laboratóriumok közötti távolság jó nagy és így van idő a kockadobás elvégzésére és a mágnesek beállítására. Minden egyes esetben a kísérletezők feljegyzik, milyen irányú spinvetületet mértek a három lehetséges közül és milyen előjelűnek találták azt. A kísérletet nagyon sok azonos módon preparált neutron-proton párral elvégzik, majd a két listát egymás mellé helyezik. Ugyanolyan jellegű összesített listát kapnak, mint amit az 1. táblázat tartalmaz. Az 1., 2., 3. szám mutatja, milyen irányban történt a spinvetület mérése, a P és a K pedig azt jelzi, hogy pozitívnak vagy negatívnak bizonyult-e a spinvetület az adott irány mentén.
Ebben a kísérletben valóban teljesül, hogy a táblázat azon soraiban, amelyekben mindkét szám ugyanaz, az egyik oszlopban mindig P. a másikban mindig K betűt találunk, vagyis ha mindkét kísérletező véletlenül azonos irányú spinvetületet mér, a két részecske spinvetületének előjele szükségképpen ellentétes egymással. Mint már szó volt róla, ebben jut kifejezésre az a tény, hogy a rendszer teljes spinje zérus. A táblázatnak ezek a sorai bizonyítják, hogy a két szélső laboratóriumban a kísérleti eredmények rögzítését tartalmazó makroszkopikus eseménysorok pontosan ugyanúgy nem függetlenek egymástól, mint a borítékos kísérletben, és nyilvánvalónak látszik, hogy a korreláció csak közös ok típusú lehet. De akkor a részecskéknek hordozniuk kell valami olyan sajátosságot, amely spinvetületekre vonatkozó információt képes tárolni. Erről a sajátosságról semmilyen konkrét ismeretünk sincs, csak annyit tudunk róla, milyen típusú információt kódol. Ennyi azonban már elegendő ahhoz, hogy minden neutron-proton párt a 2. táblázat négy típusának valamelyikébe sorolhassuk be: pl. a d. típusba kell sorolni azt a párt, amelyben az egyik részecske olyan, hogy az n1 és az n3 irányú spinvetületének mérésénél pozitív, az n2 irányúnál negatív mérési eredményt kapnánk.
Az előző fejezetben tárgyalt módon a wa, wb, wc, wd valószínűségek segítségével kifejezhetjük a p(1P,2P), p(2P,3P), p(1P,3P) valószínűségeket és levezethetjük a 3-as Bell-egyenlőtlenséget. Ha a részecskékben van valamilyen tulajdonság, amely a korrelációt biztosító információt kódolja, ennek az egyenlőtlenségnek teljesülnie kell.
A Bell-egyenlőtlenség ellenőrzéséhez nem feltétlenül szükséges a kísérlet tényleges elvégzése, ha elfogadjuk, hogy a kísérlet úgyis azt adná, amit a kvantumelméleti formulák alapján előre ki tudunk számítani. A kvantumelmélet szerint annak q(n, n’) valószínűségét, hogy egy S = 0 állapotú pár egyik részecskéjének a spinvetülete egy bizonyos n irányban ugyanolyan előjelű, mint a másik részecske spinvetülete egy tetszőleges másik n’ irányban, a
q(n, n’) = 1/2 ∙ (1 – cos ϑ)
képlet adja meg, ahol ϑ az n és az n’ által bezárt szög. A közös előjel 1/2 valószínűséggel lehet pozitív vagy negatív. Annak q̄(n, n’) valószínűsége pedig, hogy e két vetület előjele különböző, nyilván
q̄(n, n’) = 1 – q(n, n’) = 1/2 (1 + cos ϑ)
-val egyenlő. Ha pl. n = n’ , akkor q = 0, q̄ = 1, ahogy egy S = 0 párnál lennie is kell.
Ezeknek a képleteknek az alapján
p(1P,2P) = 2/9 ∙ 1/2 ∙ q(n1,n2) = 1/18 ∙ (1 – ϑ12)
p(2P,3P) = 2/9 ∙ 1/2 ∙ q(n2,n3) = 1/18 ∙ (1 – ϑ23)
p(1P,3P) = 2/9 ∙ 1/2 ∙ q(n1,n3) = 1/18 ∙ (1 – ϑ13)
A 2/9 tényező a mérési irányok véletlen megválasztásával kapcsolatos (az első sorban például 2/9 annak a valószínűsége, hogy az egyik kísérletező n1, a másik n3 irányú spinvetületet mérjen). Ha ezeket a kifejezéseket a 3-as Bell-egyenlőtlenségbe írjuk, az
| 1 + cos ϑ13 ≥ cos ϑ12 + cos ϑ23 | [4] |
egyenlőtlenségre jutunk, amely nem teljesül három tetszőleges irányra. Legyen például mindhárom irány ugyanabban a közös síkban, az n1 és az n3 közötti szög legyen ϑ13 3π/4, az n2 ossza ezt a szöget 2:1 arányban (ϑ12 = π/4, ϑ23 = π/2). Akkor (ϑ12 = -cos ϑ13 = 1/√2), cos ϑ23 = 0 és a 4-es egyenlőtlenség 1/√2 alakú lesz, ami nyilván nem igaz.
A neutronban és a protonban tehát nincs olyan tulajdonság, amely lehetővé tenné, hogy az S = 0 állapotú rendszerben tapasztalható spinkorrelációt közös okkal magyarázzuk azon az alapon, hogy a spinvetületek közötti összefüggés már a neutron és a proton szétválásának a pillanatában eldőlt. Az egyenes irányú korrelációt is kizárhatjuk, hiszen ehhez az kellene, hogy az egyik vetületmérés eredménye határozza meg a másikat, de ha a két szélső laboratórium a középsőtől azonos távolságra van, ennek az információnak pillanatszerűen, végtelen nagy sebességgel kellene terjednie. A spinkorrelációk értelmezéséhez tehát ez a két intuitív determinációs forma elégtelen – harmadikat viszont nem tudunk elképzelni.
A Stern-Gerlach berendezéssel egyszerre csak egy irányú spinvetület előjelét tudjuk meghatározni, ez a körülmény összhangban van azzal, hogy a különböző irányú spinvetületek operátorai nem kommutálnak egymással. Az előző fejezetben ezt a tulajdonságot imitálta az a tilalom, hogy csak az egyik kis borítékot lehetett felbontani. A spinek esetében azonban nem önkényes tilalomról, hanem természeti törvényről van szó. Ezért nem tudjuk igazolni az előző fejezet gondolatmenetével pusztán logikai úton a Bell-egyenlőtlenség teljesülését. De ettől még teljesülhetne! Ha így volna, akkor abból, hogy két fizikai mennyiség nem mérhető egyszerre, nem következne, hogy a mérési objektumban nincsenek olyan tulajdonságok, amelyek a mérési eredményt determinálják. Csak annyit mondhatnánk, hogy nem lehet valamennyi tulajdonságot egyszerre felismerni. Ezeket a hipotetikus tulajdonságokat szokás rejtett paramétereknek nevezni. A Bell-egyenlőtlenség sérülése azonban azt mutatja, hogy a kvantumelmélet nem engedi meg rejtett paraméterek létezését, vagyis a mérés eredménye legalább is bizonyos esetekben magának a mérésnek a következtében jelenik meg az objektumban az elmélet valószínűségi törvényeinek megfelelő eloszlásban.
A helyzet valójában még egy fokkal bonyolultabb. Tegyük fel, hogy mondjuk a jobboldali laboratórium sokkal nagyobb távolságban van a középsőtől, mint a baloldali. A mérési eredmények táblázata ettől nem változik meg és továbbra is igaz lesz, hogy azokban az esetekben, amikor mindkét laboratóriumban véletlenül ugyanabba az irányba eső spinvetületet mérnek, a két mérési eredmény előjele mindig különböző. Ez annyit jelent, hogy ha a baloldali laboratóriumban mondjuk pozitív vetületet kapunk, akkor bizonyosak lehetünk benne, hogy a jobboldali laboratóriumban későbbi időpontban elvégzendő mérés negatív vetületet ad majd. De az előbb megállapítottuk, hogy a baloldali laboratóriumban végzett mérés eredménye a mérés következtében jött létre, nem volt rejtett paraméter segítségével kódolva a részecskében. Ezért el kell fogadnunk, hogy a jobboldali laboratóriumban elvégzendő mérés eredménye ugyancsak a baloldali laboratóriumban végrehajtott mérés következménye. A kvantumelmélet szerint tehát nemcsak az igaz, hogy a mérés során bizonyos tulajdonságokat hozunk létre abban az objektumban, amelyre közvetlenül hatunk a mérőeszközzel, hanem egyes esetekben elég a rendszer egyik részére hatni ahhoz, hogy a tőle tetszőlegesen nagy távolságban levő másik rész állapotát is befolyásoljuk.
Ha ezt a jelenséget fel lehetne használni információ továbbítására az A és a B között, akkor ez – a relativitáselmélet követelményével ellentétben – fénynél gyorsabban (pillanatszerűen) terjedő hatás volna. Megmutatható azonban, hogy erre nincs lehetőség, mert nem a kísérletezők választásán múlik, milyen előjelűnek adódik a részecske spinvetülete a Stern-Gerlach berendezésen történő áthaladás során.
Bell-egyenlőtlenségeket fotonokkal végezhető spinkorrelációs kísérletekben is megfogalmazhatunk. Az ilyen kísérleteket technikailag könnyebb megvalósítani, mint azokat, amelyekhez neutron-proton párok szükségesek, ezért a Bell-egyenlőtlenségek ellenőrzését célzó ma már igen pontos méréseket fotonpárokkal végezték el. Gyakori jelenség, hogy egy atom valamelyik gerjesztett állapota fotonkibocsátással nem közvetlenül alapállapotra, hanem egy közbeeső gerjesztett állapotra bomlik le és az atom csak egy második foton emissziója után kerül alapállapotba. Ha az atomi állapotok spinjét ismerjük, a kvantumelmélet alapján kiszámíthatjuk a fotonok polarizációja közötti korrelációt. Ez a korreláció általában megsérti a Bell-egyenlőtlenségeket, és mint azt a részletes analízis bizonyítja, ez a tény még akkor is megállapítható, ha figyelembe vesszük a reális kísérletekben elkerülhetetlen torzításokat is. A kísérletek a kvantumelméleti jóslatok helyességét és így a Bell-egyenlőtlenségek sérülését igazolják, így ma már aligha kételkedhetünk abban, hogy a természet él olyan determinációs formákkal, amelyek kívül esnek szemléletünk keretein.
Összefoglalás – ismeretelméleti megjegyzések
Analízisünk eredményét még úgy is megfogalmazhatjuk, hogy a kvantumjelenségek körében a valószínűségnek bizonyosságba való átfordulása más természetű, mint a klasszikus jelenségek viszonyai között. Ha egy kockát feldobunk és nem nézzük meg, hogyan esett le, az egyes kimeneteleknek csak a valószínűségét ismerjük. Elég rápillantanunk a kockára ahhoz, hogy ez a valószínűség bizonyossággá változzon át. Nyilvánvaló, hogy a változás nem a kocka állapotában, hanem a tudásunkban következett be. A kvantumelméletben is ez lenne a helyzet, ha a mérés csak már meglevő tulajdonságokat hozhatna felszínre. A Bell-egyenlőtlenség sérülése azonban arra utal, hogy maga a megfigyelés hozza létre az észlelt tulajdonságot, tehát a valószínűségnek bizonyossággá történő átváltozása nem interpretálható kizárólag a tudásunkban bekövetkezett változásként. De a mérőeszköznek az objektumra gyakorolt fizikai hatásával sem magyarázható kézzelfogható módon, hiszen – mint az előző fejezetben láttuk, – egy részrendszeren végzett megfigyelés képes előidézni a valószínűségnek bizonyosságba történő átfordulását a rendszer tetszőlegesen nagy távolságban lévő másik részén is.
Ez a paradox sajátosság úgy is kifejezhető, hogy a kvantumelméletben egyetlen egységnek (vagyis egy rendszernek) kell tekinteni minden olyan rendszert, amelynek elemei valamikor közvetlen kölcsönhatásban voltak, függetlenül attól, hogy időközben a részek eltávolodtak egymástól. Ezt a megfogalmazási módot gyakran tekintik a paradoxon magyarázatának, pedig csak implicit kifejezése annak az állításnak, hogy egy részrendszeren végzett megfigyelés befolyást gyakorolhat egy térbelileg jól elkülönített másik részrendszer állapotára is.
De mi szorul itt tulajdonképpen magyarázatra? A paradoxon a Bell-egyenlőtlenség sérülése miatt jött létre, a Bell-egyenlőtlenség viszont azért sérül, mert a mérések igazolják a kvantumelmélet valószínűségi formuláit. De ha a kvantumelmélet helyesen írja le a tapasztalati anyagot, mi az, amit még meg kell magyarázni?
Valóban, nincs alapos okunk kételkedni abban, hogy a jelenségeknek arról a köréről, amelyhez a spinkorreláció is tartozik, a kvantumelmélet a tapasztalatnak megfelelően képes számot adni. Azonban mint a tudományos elméletek általában, a kvantumelmélet is az emberi megismerési folyamat terméke, és nemcsak a megismerés objektumának, a mikrovilágnak a sajátosságait tükrözi, hanem a megismerő szubjektumét is. A Bell-egyenlőtlenség sérülése a szubjektum-objektum kapcsolat mikéntjére vonatkozóan jelent olyan problémát, amely magyarázatra, vagy legalább is gondos körülírásra szorul.
A megismerési folyamat eredménye felfogásunkban spontán módon rendeződik el olyan különböző kategóriák szerint, mint a tér és az idő, vagy azok a determinációs formák, amelyekről az előzőekben annyi szó esett. A klasszikus fizika különböző ágai konkrét tartalmuktól függetlenül képesek úgy leírni az érvényességi körükbe tartozó jelenségeket, hogy közben nem kerülnek összeütközésbe ezekkel a kategóriákkal. Ennek valószínűleg az az oka, hogy az emberré válás folyamatában pont azok a kategóriák épültek be a tudatunkba valamilyen ma még teljesen ismeretlen módon, amelyek a valósággal harmonizálva rendezték össze az emberméretű klasszikus világban szerzett tapasztalatokat és ezért túlélési értékük volt.
Már a kvantumelmélet megalkotásának egészen korai periódusában felismerték, hogy ennek az elméletnek a szerkezete nem illeszthető be közvetlenül tudati kategóriáink keretei közé. Ezt a “kategoriális elégtelenséget” fejezi ki például a hullám-részecske dualizmus, vagy általánosabban az a tény, hogy egy adott mikroobjektumot különböző körülmények között csak különböző, egymásnak ellentmondó képek segítségével tudunk intuitív módon magunk elő képzelni, annak ellenére, hogy a matematikai leírás ellentmondásmentes. Jogos azonban feltenni azt a kérdést, hogy a mikrojelenségeknek ez a konfliktusa az alapfogalmainkkal levonható-e közvetlenül a mérési tapasztalatból, vagy pedig csak akkor lép fel, amikor a tapasztalati anyagot a kvantumelmélet alapján interpretáljuk. Az a tény például, hogy egy radioaktív atom minden irányban egyenlő valószínűséggel emittálhatja az alfa-részecskét, egyáltalán nem ütközik a szemlélettel. Ellentmondás csak a kvantumelméleti leírás képszerű megjelenítésén belül jön létre, amely szerint az alfa-részecske hullámfüggvénye egy minden irányban egyszerre szétterjedő gömbhullám annak ellenére, hogy a részecskét mindig egészben, egyetlen határozott irányban detektáljuk. Ha minden kvantumelméleti ellentmondás ilyen természetű volna, akkor egyáltalán nem lehetne kizárni, hogy az adott tapasztalati anyagot esetleg egy olyan ma még ismeretlen elmélettel is le tudnánk írni, amelynek a formalizmusa összefér a szemlélettel.
A Bell-egyenlőtlenség jelentősége abban van, hogy olyan ellentmondást tár fel, amely bizonyosan nem a kvantumelméleti interpretáción belül jön létre, hanem azt fejezi ki, hogy a nyers tapasztalati anyag nem fér össze azzal az intuitív meggyőződésünkkel, hogy távoli eseménysorok tartósan csak akkor lehetnek korreláltak, ha ezt a korrelációt valamilyen információ terjedése képes megmagyarázni. Noha az ilyen típusú jelenségek a kvantumelmélet alkalmazási körének csak egy részét ölelik fel, mégis nagymértékben megerősítenek abban a meggyőződésünkben, hogy a kvantumelméleti interpretáció szemléleti nehézségei a mikrovilág objektív sajátosságait tükrözik.
Jegyzetek
- Ez lenne a helyzet pl. akkor, ha a korong színe attól függne, hogy nitrogén vagy oxigén molekula ütközik elsőként bele a kis boríték felnyitása után.
- John Stuart Bell 1955-ben a birminghami egyetemen doktorált a térelmélet invariancia-problémáiról írott dolgozatával. 1959 óta a CERN állandó munkatársa. Nevét kvantumtérelméleti és kvantumelméleti munkássága tette ismertté. A róla elnevezett egyenlőtlenségekkel kapcsolatos eredményei jórészt 1964-ben, kaliforniai kiküldetése idején születtek.







