Teleportáció

Van-e esélye egy közönséges halandónak arra, hogy egy tudományos tényként előadott, de hihetetlennek tűnő hírt mélyebben megértsen, lehámozza a szenzációhajhász maszlagot és felfedezze a mélyben rejtőző gyöngyszemet? A csodát, amely talán nem váltja meg az emberiséget olyan módon, ahogy azt az eredeti tudósítás előadta, de amely rávilágít a tudomány egy-egy meglepő megállapítására vagy rejtélyére. Olyan problémákról van szó, amik láthatóan érdeklik a közvéleményt, mint a teleportáció, a vákuumenergia felhasználása vagy a fénysebesség elérhetetlensége. Mindezekről a tudománynak igen sok mondanivalója volna, ezek mégsem jutnak el a laikusokig, akik így a nemtudományos irányzatokban lelnek magyarázatot kérdéseikre.
“Beam me up, Scotty”
Be kell vallanom, hogy a cikk csak Kirk kapitány miatt keltette fel az érdeklődésemet. Elfelejtettem olvasnivalót vinni a repülőútra, így belelapoztam a mindig kéznél levő légi újságba: Bordbuch (June 1998 – Tyrolean Airways). “Beam me up, Scotty!” – “Átsugárzást kérek Scotty!” villant a szemembe a nagy szalagcím, és én felkészültem egy jó kis Star Trek féle sci-fire (A gyengébbek kedvéért említem meg, hogy a magyarul Űrszekerek címen futó sorozatban egy speciális készülékkel sugározták le magukat az asztronauták a bolygókra, illetve onnan vissza az űrhajóra). Nos, kaptam is néhány izgalmas háttérinformációt kedvenc sorozatomról, de ahogy belemelegedtem, rá kellett döbbennem, hogy itt bizony új tudományos szenzációval kínálnak. Nem is akármivel! A Der Spiegelre hivatkozó cikk szerint a neves osztrák fizikus, Zeilinger és csapata valódi teleportációt valósított meg – igaz egyenlőre csak elemi részecskékkel.
Talán mosolyogva abbahagytam volna az olvasást, ha nem jut eszembe, hogy néhány nappal azelőtt egy műszaki végzettségű munkatársam jelentette ki az ebéd utáni társalgás közben, hogy a teleportáció immár bizonyított tény. Elmondása szerint mikroszkopikus testeket (!) egyik városból a másikba teleportáltak. Akkor póker arccal siklottam el a bejelentés felett (ugyanúgy nem tudtam cáfolni a hírt, mint ahogy a munkatársam sem tudta volna érvekkel alátámasztani azt), de most már kezdett a dolog érdekelni. Az utazás után visszatértem a témára a munkahelyemen, de a kolléga nem tudta, hogy hol olvasta a hírt, és az említetteken kívül másra nem is emlékezett. Ennek ellenére számára a teleportáció immáron bizonyított, sőt technikailag megvalósított ténnyé lépett elő.
Van-e lehetősége egy nem “beavatott” embernek az ilyen híradásokat leellenőrizni? Bármi is az eredmény, a “hitetlen” ember csak nyerhet. Vagy jobban megérti a jelenséget és a társágban büszkén villoghat frissen szerzett tudásával, vagy biztos háttérrel szállhat szembe az álhírrel következő alkalommal. Ráadásul az agytorna önmagában is élmény.
Hogyan is vágjak neki? Néhány éve már itt elakadtam volna, de most ráakaszkodtam az Internetre, és az Altavista keresőn rákerestem a “teleportation” szóra, majd az említett fizikus nevére: “Zeilinger”. A találati lista ugyan vegyes volt, de számomra meglepő módon nem a paratudományos, hanem a – hogy is mondjam – konvencionális tudomány lapjai (linkjei) domináltak. A találatok közt volt populista cikk a New Scientist-ből (ennek fordítását megtaláltam a Természet Világában is), egy “keresztény-tudományos” társaság próféciákkal és paratudományokkal foglalkozó lapja (először ezen keresztül jutottam el Anton Zeilinger honlapjára!), a többi jórészt szakcikk. Kedves, de megtévesztő módon Zeilingerék honlapjáról link vezetett a Star Trek őrültek (angolul ezt szebben mondják: Star Trek fan) saját lapjára. A komolyan vehető anyagok közül egyedül a könnyedebb New Scientist cikkben említették, hogy néhány évtizeden belül esetleg atomok, molekulák, sőt kis vírusok is teleportálhatók lehetnek (Az információ torzulásának demonstrálása céljából érdemes megemlíteni, hogy a Természet Világa fordításában a kutató már szentül meg volt győződve erről a lehetőségről). Az összes többi cikkben, amelyek a – most már nevezzük a nevén – kvantum teleportáció elméletét és megvalósítását tárgyalták, sehol sem találtam utalást másra, mint a fotonok, neutronok és esetleg a jövőben atomok kvantumállapotának teleportálására.
Kvantum teleportációs kísérletek
A találatok átnézése közben hamar rátaláltam az Insbrucki Egyetem Kísérleti Fizika Tanszékén Anton Zeilinger csapatának lapjaira[…]. Postscript file formátumban letölthető és kinyomtatható a “légi újságban” hivatkozott kísérletükről szóló Nature cikk (tucatnyi egyéb közleménnyel egyetemben). A kísérlet részletes összeállítása, a hozzá felhasznált eszközök listája fényképekkel, magyarázatokkal és hasznos linkekkel megtalálható a Foton Laboratórium oldalain. Az élmény fantasztikus! Alig néhány órával ezelőtt egy pletyka és egy kicsit szenzációhajhász – bár utólag átnézve szakmailag korrekt – cikk alapján indultam el, és most szinte megtapogathatom a kísérleti eszközöket. Fényképeken látom a berendezésekkel zsúfolt szobákat, a kísérletben használt több száz méternyi optikai kábel útvonalát az alagsorban és a serénykedő szerzőket. A nyitottság ezen élménye annyira ellentétes némely paratudós elmélkedésével a tudósvilág titokzatos összeesküvéséről és titkolózásáról, hogy szinte kukkolónak érzem magam a számítógépem előtt ülve. Kétségbeesett kapkodással töltöm le a megtalált anyagot és csak később jövök rá, hogy erre semmi szükség. Egy könyvjelzőt helyezek el, így bármikor újból meglátogathatom az érdekesebb oldalakat egy kattintással.
Megtaláltam egy másik csapat kísérleteinek adatait is. Ők a Physical Review Letters-ben jelentették meg cikküket. A Hewlett-Packard Laboratories-ban lehet letölteni róla részletes anyagot. Mindkét kísérlet alapja egy elméleti ötlet, amelyet az IBM-nél dolgoztak ki. Mindenhol EPR paradoxonról és EPR csatornáról lehet olvasni. Mint hamar kiderül, ez az Einstein-Podolsky-Rosen hármast jelenti. Paradoxon és Einstein! Ez jóval kecsegtet. De egy kicsit fogjuk vissza magunkat! Már itt is elég sok F meg Y keveredik feles spinekkel. Anélkül, hogy mélyebbre mennénk ki kellene deríteni, hogy mi ez a teleportáció, amiről itt beszélnek. Vessük össze a könnyedebb anyagokat a kísérletek leírásával, vagy legalábbis utóbbiak ábráival, bevezetőjével és összefoglalásával.
Mint kiderül a kérdés az, hogy lehet-e egy foton állapotát átvinni egy másik fotonra (a fotonnak a terjedési irányán kívül gyakorlatilag csak a polarizációja a szabad paraméter). Bizonyított tény, hogy egy elemi részecske állapotát egy másikra átmásolni nem lehet. Azaz, ha van egy bizonyos paraméterekkel rendelkező P fotonunk, akkor sehogy sem tudjuk elérni, hogy egy másik R foton szinte a P klónjaként átvegye annak tulajdonságait és ezzel két teljesen egyforma részecskét kapjunk. Az IBM-esek ötlete azon alapul, hogy a tulajdonságot nem átmásoljuk, hanem átvisszük P-ről R-re, miközben az P foton állapota drasztikusan megváltozik. Ez már nem ellenkezik a kvantumelmélet szabályaival. Számítógépes hasonlattal élve copy-paste nem megengedett, de cut-paste elméletileg igen.
Egy nagyon fontos dolgot le kell szögezni. Nincs szó egyáltalán anyag teleportációjáról. Nem tűnik el anyag valahol, hogy aztán máshol a semmiből előtűnjön. Egy létező elemi részecske állapotát (tulajdonságait) visszük át egy másik már létező elemi részecskére. Mivel a kvantumállapot átviteléhez nem szükséges, hogy a két elemi részecske egymás közelében legyen – akár igen nagy távolpságra is lehetnek egymástól , az effektust elnevezték kvantum teleportációnak (quantum teleportation). A félreértések tömegéhez vezető szerencsétlen elnevezés hatására a következő fejezetben visszatérek.

1. ábra – A kvantum-teleportáció elvi sémája
Az elméleti kísérletben az A helyen levő P foton állapotát szeretnénk átvinni a legalább néhány méternyi távolságban lévő B hely R fotonjára. A két helyen levő kísérletezőt szokás szerint Alice-nak és és Bob-nak nevezik (1. ábra). Alice laborja elég zsúfolt. Valamilyen forrásból kapja az ismeretlen állapotú P fotont. Egy másik szerkezet egy speciális fotonpárt (Q és R) bocsájt ki. A P és a Q fotonokat Alice egy mérődobozban összeereszti (a két foton kvantumállapotai szuperponálódnak), és egy mérést végez el rajtuk. A mérésnek négy lehetséges kimentetele van, jelöljük ezeket 1, 2, 3 és 4-nek. Bob megkapja a R fotont és Alice mérésének eredményét valamilyen konvencionális módon (mondjuk vezetéken két bit-nyi jel formájában). Ekkor Bob a nála elhelyezett szerkezet segítségével a megkapott jelnek megfelelő transzformációt hajtja végre az R fotonon. A mérőeszköz egyes állásánál semmilyen transzformációt nem kell vérehajtani. A 2, 3 illetve 4 állásnál rendre az x, y illetve z tengelyek körül kell 180 fokos elforgatást elvégezni. Ha minden jól lett kivitelezve, akkor a transzformáció után az R foton kvantumállapota megegyezik azzal az állapottal, amellyel P foton rendelkezett a kísérlet előtt.
Az insbrucki Zeilinger csapata végrehajtotta a kísérlet egyszerűsített formáját (2. ábra). A kísérlet végén valahogy ellenőriznünk kell, hogy a transzformált R foton polarizációja megegyezik-e a P foton eredeti polarizációjával. Ezért nem ismeretlen állapotú fotonokat használunk a kísérlethez. A kiinduló P foton polarizációját Alice egy polárszűrővel megadott irányba állítja. Bob a R foton elé egy másik polárszűrőt helyezve ellenőrizheti, hogy a végeredményként kapott foton állapota megegyezik-e a kiindulási foton állapotával. Szüksége van még Alice-nak a mérőeszközre, és Bobnak a transzformálóeszközre. Zeilingerék egy olyan mérőeszközt tudtak összeállítani, amely a lehetséges négy állapotból csak az egyes állapotot tudta biztosan elkülöníteni. Ehhez a mérőálláshoz pont nem tartozik transzformáció, így a transzformáló eszközt ki is hagyták.
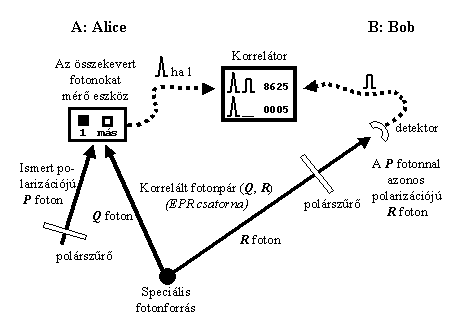
2. ábra – Egyszerűsített kvantum teleportációs kísérlet
Természetesen ilyen körülmények között a kvantumállapot transzportációja csak azokban az esetekben sikerül, amikor Alice mérőeszköze egyest mér (egyéb esetekben szükséges lenne valamelyik transzformáció). Ez statisztikusan az esetek 25%-ban fordul elő. Bob polarizátora úgy van beállítva, hogy a P-vel azonos állapotú fotont engedje át. Tehát minden esetben, amikor Alice egyest mér, Bob detektora meg kell hogy szólaljon. Ha ebben az esetben Bob detektora nem szólalna meg, az azt jelentené, hogy a kvantumállapot (polarizáció) átvitele nem történt meg.
Az elvégzett kísérletek teljes összhangban vannak a kvantumelmélet jóslataival. Az érdekesség abban van, hogy egy elemi részecske – akár nem is ismert – kvantumállapotát két részben visszük át. Az 1. ábrán ábrázolt teljes megvalósításban egyfelől használunk egy szokványos információátviteli csatornát, amin ebben az esetben két bitnyi információt viszünk át. A kvantumállapot maradék részét a korrelált állapotú fotonpár viszi át.
Mit szólna ehhez Kirk kapitány?
Teleportáció-e ez, vagy sem? Ennek eldöntéséhez azt kell meghatároznunk, hogy mit is jelent számunkra a teleportáció kifejezés. Egyetlen erről szóló elmélkedést találtam, de az kedves és elfogadható. Az IBM-es csapatba tartozó Braunstein szerint az első megközelítés a következő lehet:
“A teleportáció valamilyen azonnali testetlen átvitel”
A relativitáselmélet szerint a fénysebesség mindenképpen korlátot szab a sebességre. Ennek ellentmondó tényt a mai napig nem találtak. A bemutatott kvantumteleportációs kísérletben sincs azonnali átvitel. Mind az R fotonnak, mind a két bitnyi információnak időre van szüksége, hogy A-ból B-be érjen. Tehát egyenlőre maradjunk annyiban, hogy…
“A teleportáció valamilyen testetlen átvitel”
Eszünkbe juthat itt akár a telefon, vagy a TV is, de hát azokban az esetekben nem a tényleges test kerül át. Van viszont egy – igaz megint csak mikroszkópikus – igazán jó példa, az alagúteffektus. Egy elemi részecske átkerülhet egy olyan (potenciál-) falon, amelyhez egyébként nincs elég energiája. Itt eltűnik, ott megjelenik. Ez aztán tényleg teleportálódott. Elvileg akár egy kődarab is bejuthat egy bezárt szobába anélkül, hogy betörné az ablakot. Ennek azonban olyan kicsi a valószínűsége, hogy jóval hosszabb időt kéne rá várni mint az univerzum teljes életkora. És ráadásul irányítani (befolyásolni) sem tudjuk. Tehát újabb ötletként:
“A teleportáció valamilyen irányítható, testetlen átvitel”
Gondolom az egész akkor érdekes, ha valami hasznosabb dolgot tudunk átvinni, nem csupán egy-egy elemi részecskét, így…
“A teleportáció makroszkopikus testek irányítható, testetlen átvitele”
No, igen! Ez már Kirk kapitánynak is tetszene. Mi a helyzet a kvantum teleportációval? Nos, itt mindenképpen elemi részecskék átviteléről van szó. Tekinthetem magamat természetesen elemi részecskék rendezett halmazának, talán valamilyen értelemben még elméletileg létezik is valami olyan, mint az én kvantumállapotom, de ezzel még nem vagyunk közelebb. A kvantumteleportációnak szüksége van konvencionális anyag- és információátvitelre. A kísérletben is egyetlen foton “transzportálásához” át kellett ténylegesen vinnünk az R fotont és még két bit információt is. Ha tényleg egy a P foton állapotának megfelelő fotonra lenne szüksége Bobnak, akkor sokkal egyszerűbb lenne megkérni Alice-t, hogy küldje át magát a P fotont, mint végigcsinálni az egész hercehurcát a mérőeszközzel, az EPR fotonpárral és a transzformáló eszközzel. Összetettebb részecskék és nagyobb távolságok esetén a feladat olyan mértékben bonyolódik, hogy a módszer használhatatlanná válik. Gondoljuk el: egy makroszkopikus test nem csak fotonokból áll. Rengeteg anyagot kellene nagyon rendezetten korrelált EPR páronként átvinni barátságtalan – nem laboratóriumi – körülmények közt. A mérőeszköz (valami speciális szkennerszerűség) hihetetlenül bonyolult lenne, nem is beszélve a transzformáló eszközről! Azt hiszem, ezt nem is kell tovább ragozni.
Ahogy “légi újságom” a szenzációhajhász főcím “Sugározz le, Scotty!” mellett az alcímben korrektül írta: “Kirk kapitánynak még várnia kell…”
Einstein paradoxona
Ha már ennyi anyagot összegyűjtöttem, akkor érdemes lenne egy kicsit visszatérni Einsteinre és az EPR paradoxonra. Amint Schrödinger megalkotta a kvantumelmélet (a továbbiakban KE) alapjait alkotó egyenletét, Einstein azonnal felismerte, hogy az egyenlet speciális esetben olyan eredményt adhat, ami nehezen egyeztethető össze fizikai világképünkkel. Az alábbiakban didaktikai okokból nem az Einstein és társai által felvetett gondolatkísérletet elemzem, hanem egy olyan kísérletet, amely viszonylag egyszerűen el is végezhető.
A KE szerint az, hogy egy foton átmegy-e egy polárszűrőn, csak abban a pillanatban dől el, amikor odaér. Mintha a foton feldobna egy pénzdarabot és a “fej” esetén átmenne, az “írás” esetén pedig nem. A “fej” illetve az “írás” valószínűsége csak attól függ, hogy az érkező foton polarizációjának síkja mekkora szöget (Φ) zár be a polárszűrő irányával. A Schrödinger egyenlet szerint ezek a valószínűségek a következők:
p(átmegy) = cos2(Φ)
p(elakad) = sin2(Φ) = 1 – cos2(Φ) = 1 – p(átmegy)
Amennyiben a foton polarizációs síkja egybeesik a polárszűrő irányával (Φ=0°), akkor az átjutás valószínűsége egy, míg ha arra merőleges (Φ=90°), akkor az átjutás valószínűsége nulla.
Az új egyenlettel lehetővé vált olyan két-részecskés rendszerek leírása, amelyben a részecskék eredetileg nagyon közel voltak egymáshoz, vagy egy közös folyamat során keletkeztek, majd tetszőlegesen távol kerültek egymástól. Például ilyen fotonpárok keletkezhetnek a “parametric down conversion”-nek nevezett folyamat során. A keletkezett fotonok (Q és R) egymáshoz képest mindig merőlegesen polarizáltak. Ha Alice és Bob méréseket végez ezeken a fotonokon, akkor az egy fotonpárhoz tartozó mérések nagyon erős korrelációt fognak mutatni. Egymásra merőlegesen beállított polárszűrők esetén vagy mindkét foton át fog menni a saját polárszűrőjén, vagy egyik sem (lásd a 3. ábrát).
Képzeljük el, hogy a két megfigyelőhely (A és B) egymástól 150 millió kilométerre van egymástól, ami nagyjából a Föld-Nap távolsággal egyenlő. A speciális fotonforrás legyen valahol közöttük egy űrhajón úgy, hogy Alice-hoz a Q foton egy perccel hamarabb érjen el, mint Bob-hoz az R foton. Így Alice egy perccel hamarabb el tudja végezni a mérést min Bob. Ezzel megtudja, hogy a foton átment-e az ő polárszűrőjén, vagy sem. A teljes korreláció miatt már ekkor teljes bizonyossággal meg tudja mondani, hogy mit fog mérni Bob (t.i. ugyanazt, mint ő). Bob csak egy perc múlva fogja ugyanezt megtudni, miután az ő fotonja megérkezett, és a mérést elvégezte rajta.
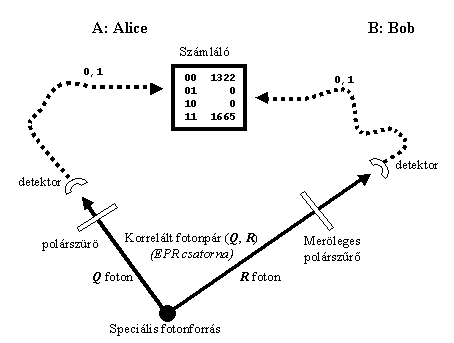
3. ábra – Korrelált fotonpár (entangled photon pair)
A KE által megjósolt, és a kísérletek által egyébként igazolt teljes korreláció háromféleképpen magyarázható:
- Tekintsük tényleg valóságnak azt, ahogy a KE hullámfüggvénye leírja az esetet. Egyetlen hullámfüggvény írja le egyszerre mindkét foton viselkedését, tehát nem két független fotonról van szó, hanem egy fotonpárról. A fotonpár akkor is egyetlen valós egység marad, ha részei (a két foton) egymástól akármilyen távolra kerül. Ezzel tulajdonképpen nem magyarázatot adtunk a korrelációra, hanem értelmetlenné tettük a kérdést. Amikor a fotonpár úgy dönt, hogy egyik tagja átmegy az egyik polárszűrőn, akkor ezzel együtt azt is eldöntötte, hogy a másik is átmegy. Nem két objektum létezik (a két foton), hanem csak egy (a fotonpár).
- Amikor az egyik foton dob és megkapja az eredményt, villámgyorsan tudatja azt a pár másik tagjával, akármilyen távol is vannak egymástól. A második foton ezen információ alapján dönti el, hogy átmehet-e, vagy sem.
- Ez egy misztikus távolhatás, amely a fénynél nagyobb sebességre lenne képes.
A fotonok még akkor sorsolnak, amikor együtt vannak. A kapott eredmény, mint egy gén (a fizikai paraméterért felelős valós entitás) megőrződik bennük, és akkor aktivizálódik a megfelelő viselkedést kiváltva, amikor a polárszűrővel találkoznak.
Az 1. magyarázat szerint létezhetnek olyan objektumok a világban (például a korrelált fotonok), amelyek mérete akár fényévnyi is lehet. Ez nagyon szokatlan dolog. A világot leíró törvényeink mindig lokálisak abban az értelemben, hogy az egyik helyen történő események vizsgálatakor nem kell törődnünk olyan dolgokkal, amelyek ugyanakkor egy egészen távoli ponton éppen történnek. Alice és Bob is használhatnának lokális elméletet annak leírására, hogy az ő fotonjuk hogyan viselkedik, de amikor összevetik az eredményeiket, akkor paradoxonokhoz jutnak. Lokális elméletük esetleg nem teszi lehetővé a teljes esemény együttes leírását. A korrelált fotonokat egy egészként leíró hullámfüggvény azonban nem lokális, hanem az egész térben egyszerre írja le az objektum viselkedését.
A 2. megközelítés a szokványos lokális törvényeket tételezi fel, de megengedi, hogy bizonyos hatások a fénynél nagyobb sebességgel terjedve befolyásoljanak távoli történéseket. Esetünkben az A helyről B irányában történő távolhatás egy perc alatt 150 millió kilométert megtéve legalább nyolcszoros fénysebességgel halad, ezzel előidézve a R foton megfelelő viselkedését. Biztos sokaknak meglepő, de ez önnmagában nem mond ellent a speciális relativitáselméletnek. Bár ezt így nem szokták megfogalmazni, de a speciális relativitáselmélet csak az információáramlással együttjáró folyamatok sebességmaximumát határozza meg. Itt a távolhatás a két esemény közti korrelációt valósítja meg, de információt nem hordoz. Ez azt jelenti, hogy Alice sehogy sem tudja kihasználni kedvező helyzetét (t.i. azt, hogy tőle indul ki a távolhatás) arra, hogy Bob-bal információt közöljön nyolcszoros fénysebességgel. Eleinte még a fizikusok számára sem volt tiszta ez a finom de lényegi különbség két esemény közti korreláció és a köztük meglévő vagy nem létező információáramlás közt. Így többen nekiláttak a korrelált részecskepárokon alapuló szuperlumináris (fénysebesség feletti) információtovábbító eszköz megtervezésének. Természetesen nem sikerült.
A 3. magyarázat szerint a fotonok az elválásuk pillanatától kezdve magukban hordozzák azt az információt – mint egy gént -, amelyik meghatározza, hogy hogyan viselkedjenek a polárszűrővel találkozva. Ha a Q foton azt az információt hordozza, hogy át kell mennie az ő polárszűrőjén, akkor az R foton azt hordozza, hogy egy ugyanúgy beállított polárszűrőn nem, de egy – a kísérletünknek megfelelő – merőleges polárszűrőn át kell mennie. Itt az információáramlás a speciális fotonforrás felől az A és a B pontok fele áramlik (a fotonokkal együtt éppen fénysebességgel haladva) előidézve a korrelációt. Ez tűnik a legtermészetesebb képnek. A Q foton ezt az információt hordozza, az R foton pedig amazt. A legtöbb természettudományos modellünk ilyen.
A 2. magyarázat nem is konform a világképünkkel, ráadásul nincs is semmi elképzelésünk a feltételezett távolhatás mibenlétéről, tehát tegyük egyenlőre félre. A 3. magyarázat jó volna, de ekkor a KE egyenletében lennie kéne olyan paramétereknek, amelyek konkrétan meghatározzák a polárszűrőkön való átjutást illetve elakadást mindenféle polárszűrő szögre. Ezen paramétereknek a fotonok születésétől kezdve a polárszűrővel való találkozásig változatlannak kell lenniük. Az alábbi bekezdés – talán e cikk legfontosabb részeként – ezen elvárást fogalmazza meg:
Elméleti kísérletünkben az R foton átjutásának kérdése már egy perccel a polárszűrővel való találkozás előtt eldőlt. Alice már biztosan tudta, hogy Bob mit fog mérni egy perc múlva. Az R foton már nem fog pénzt feldobni. Az átjutásról szóló információnak ezen utolsó percben meg kell őrződnie az R fotonban a polárszűrővel való találkozásig. Mivel azonban nem tételezünk fel távolhatást az A pontban lévő Q foton és a B fele haladó R foton között, ennek az információnak az R fotonban már előbb is – a foton keletkezésekor – jelen kellett lennie.
Einstein és társai (Einstein, Podolsky, Rosen = EPR) ezt az elvárást 1935-ben az alábbi módon fogalmazták meg (zárójeles megjegyzések általam):
“Ha egy rendszer (R foton) fizikai paraméterének értékét (átmegy-e a polárszűrőn) teljes bizonyossággal meg tudjuk jósolni annélkül, hogy bármilyen módon mérést végeznénk el rajta, akkor kell léteznie egy lokális tulajdonságnak (element of physical reality), ami konkrétan felelős ezért a fizikai paraméterért.”
Már EPR rámutatott arra, hogy ilyen paraméterek a hullámfüggvényben nem találhatók. Szerintük ez azt mutatja, hogy a KE – bár jól leírja a kvantumrészecskék viselkedését – nem teljes, nem a részecskék valós fizikai paraméterei alapján van felépítve. Ezen – úgy nevezett – rejtett paraméterek felismerése alapján a jövőben valószínűleg lehetséges lesz egy új kvantumelmélet (nevezzük KE2-nek) felépítése. Fontos megismételni, hogy EPR nem azt állította, hogy a KE nem jól írja le a kvantum eseményeket, hanem azt, hogy szerintük lehetséges egy teljesebb, a kvantumrészecskék tulajdonságait jobban tükröző elméletet kidolgozni. Ezen KE2 mivel az egyes részecskék saját (lokális) paramétere alapján írná le viselkedésüket egy – a KE-hez nem hasonló – lokális törvény, tehát jobban illeszkedne természettudományos szemléletünkhöz.
Bohr válaszában megvédte a KE-t és elvetette a rejtett paraméterek – azaz egy lehetséges teljesebb elmélet – létét. A vita elméleti síkon folyt, és – mivel a KE tényleg mindvégig használhatónak bizonyult – egy szűk szakmai körre korlátozódott. Érdekes megemlíteni, hogy a téma legjobbjai (J. S. Bell, A. Shimony, B. d’Espagnat és sokan mások) a 70-es évek második felében elindítottak egy írógépen szerkesztett közel havonta megjelenő “szamizdatot” is ebben a témában, nem bírván kivárni a szakmai lapok átfutási idejét.

Epistemological Letters – Hidden Variables and Quantum Uncertainty, Association Ferninand Gonseth. 1975-től 1983-ig legalább 35 szám jelent meg
A Bell egyenlőtlenségek
Az 1960-as évek elején J. S. Bell egy olyan elméleti kísérlet tervével állt elő, amellyel lehetséges volna eldönteni, hogy létezhet-e egyáltalán az EPR féle rejtett paraméteres kvantumelmélet (KE2), vagy sem (ismertetők: J.S. Bell, Hraskó P. és Hraskó P.) A terv azért szenzációs, mert egy olyan elméletről kell végső ítéletet hozni, amelyről még semmi elképzelésünk sincs. Abból az egyetlen feltevéből indul ki, hogy a KE2-ben léteznek gének, azaz esetünkben a polárszűrőn való viselkedést hordozó paraméterek.
A kísérlet nagyon hasonló az eddigiekhez. Annyi a különbség, hogy az alatt az idő alatt, amíg a foton a speciális fotonforrásból eléri őket, Alice és Bob véletlenszerűen a három előre megadott szög (a=0°, b=120o, g=240°) valamelyikébe forgatja a polárszűrőjét. Minden érkező fotonnál lejegyzik a foton sorszámát, a kiválasztott szöget és a foton viselkedését (t.i. átjutott, vagy sem). Így az 1. táblázatban ábrázolt típusú mérési jegyzőkönyveket készítik.

1. táblázat – Alice és Bob jegyzőkönyve Bell kísérletében
A kísérletsorozat végén egybevetik a jegyzőkönyveiket feljegyezve, hogy adott polárszűrőállás párnál hányszor nem jelzett egyik detektor sem (0°), hányszor csak az egyik (01 illetve 10) és hányszor mindkettő (11). A Bell által javasolt kísérlet egyszerűsített felállítását mutatja a 4. ábra.
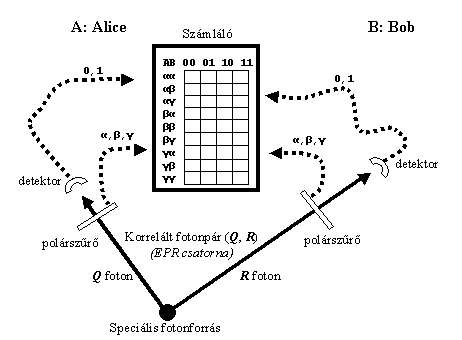
4. ábra – Aspect perdöntő kísérlete (egyszerűsítetve)
Tételezzük fel, hogy mindegyik fotonban létezik három olyan gén (paraméter), amelyek rendre azt kódolják, hogy a foton átmegy-e az α=0° szögre beállított szűrőn (α gén), a β=120° szögre beállított szűrőn (β gén), illetve a γ=240° szögre beállított szűrőn (γ gén). Az adott gén + állapota jelzi, hogy a foton átmehet és – állapota azt, hogy nem mehet át a génnek megfelelő szögben álló polárszűrőn. Azt az eddigi kísérletekből már tudjuk, hogy a speciálisan előállított kapcsolt fotonok polarizációja egymásra mindig merőleges. Tehát ha például a Q foton α génje +, azaz a Q foton úgy van kódolva, hogy az α=0° szögre beállított szűrőn átmenjen, akkor az ő R foton párjának α génje -, azaz R nem jutna át egy ugyanígy beállított szűrőn (t.i. biztosan átmenne egy erre merőlegesen beállított polárszűrőn). A 2. táblázat összefoglalja, hogy a Q és az R korrelált fotonok génkészletüktől függően hogyan viselkednek különböző polarizátorállásoknál, illetve, hogy egyenlő valószínűséggel véletlenszerűen állított polarizátorállások esetén milyen valószínűséggel jeleznek a detektorok egyformán illetve egymástól eltérően.[…] Például a harmadik sorban Q génkészlete α+β-γ+, R génkészlete ennek ellentettje α-β+γ-. Ebben a sorban az 5. oszlop azt jelenti, hogy Alice polarizátora α=0° szögre, Bob polarizátora γ=240° szögre van beállítva. A cella értéke 10 azt jelenti, hogy a génkészletnek megfelelően az A helyen a Q foton átjut a polárszűrőn (1), míg a B helyen az R foton nem jut át (0). Összesen kilencféle polarizátorállás lehet (3 x 3), ebből négy esetben viselkedik a két foton egyezően (mindkettő átjut, vagy egyik sem jut át), tehát ennek valószínűsége p=4/9 ebben az esetben (12. oszlop).
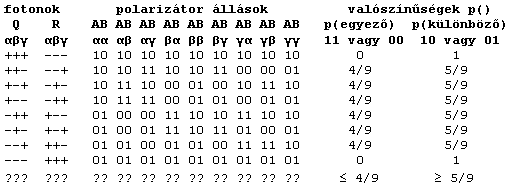
2. táblázat – A különböző génkészletű fotonpárok (első két oszlop) viselkedése különbözőféleképpen beállított polárszűrők (3-11. oszlopok) esetén. A 12. oszlop annak az eseménynek az elméleti valószínűségét adja, hogy mindkét detektor ugyanúgy jelez. A 13. oszlop az eltérő jelzések valószínűségét adja. Feltételeztük, hogy minden egyes fotonhoz Alice és Bob egyenletes eloszlással véletlenszerűen állította a polárszűrők szögét.
A fotonpárjaink génkészletét természetesen nem ismerjük. Ez lehet bármelyik a felsorolt kilencből, vagy azok valamilyen keveréke. Ez a fotonpárok előállításától függ valahogyan. A 2. táblázatot elemezve azonban nyilvánvaló, hogy a kísérlet során akárhogyan is keverednek a különböző génkészletű fotonpárok, a Q és az R fotonok az esetek legfeljebb 4/9 részében fognak megegyezően viselkedni. Tehát a rejtett paraméteres elmélet szerint egy ténylegesen elvégzett kísérletsorozatnak a következő eredményt kell adnia:
p(egyező) <= 4/9
p(különböző) >= 5/9
Ezek a mi kísérletünkre felállított Bell-egyenlőtlenségek. Felhívom a figyelmet arra, hogy semmit sem tételeztünk fel a génekről (a még nem ismert, ú.n. rejtett paraméterekről), csak azt, hogy léteznek.
A fizikusok az eddig minden valós (bizonyítható) esetben bevált kvantumelméleti hullámfüggvényeket bevetve szintén megjósolhatják az eredményt. Anélkül, hogy a bonyolult számításokba belemerülnénk, higyük el nekik, hogy a fent leírt kísérletnek szerintük (azaz a KE szerint) a következő eredménnyel kell zárulnia:
p(egyező) = p(különböző) = 1/2
Vegyük észre, hogy a két elméleti alapról kiinduló jóslat oly mértékben különbözik egymástól, hogy egy megfelelően elvégzett kísérlettel eldönthetjük, hogy melyik elmélet a helyes (melyik magyarázza meg a kísérlet eredményét). Megemlítem, hogy α, β és γ más értékeinél nem feltétlenül ad a KE a rejtett paraméteres elmélettel (KE2) ellentmondó eredményt. Még szerencse, hogy vannak ilyen speciális eredményt adó szögértékek. Elképzelhető lett volna, hogy nem találunk ilyen szituációt. Ez esetben nem lehetne kísérlettel eldönteni, hogy melyik elmélet a helyes.
Alain Aspect és társai 1982-ben elvégezték a kísérletet. Az azóta többek által megismételt kísérlet teljes mértékben igazolta a kvantumelmélet (KE) helyességét és egyben cáfolta egy olyan KE2 elmélet lehetőségét, amely génekkel (még nem ismert, rejtett paraméterekkel) magyarázza a kapcsolt részecskepárok viselkedését.
Ebben az esetben Einsteinnek és társainak nem volt igaza. Bármennyire is ellentmond eddigi szemléletünknek, az elemi részecskék világában léteznek olyan objektunok (például a speciálisan előállított korrelált fotonpárok), amelyek lokális törvényekkel nem írhatók le. A KE hullámfüggvénye azonban – mint a nem lokális elméletek talán egyedülálló képviselője – ezeket az eseteket is sikeresen kezeli.
Összefoglalás
A tudósok – sajnos – most sem fedezték fel a teleportáció megvalósításának lehetőségét – legalább is abban az értelemben, ahogy mi laikusok értelmezzük a “távolba továbbítást” -, de ismét kísérleti bizonyítékokat találtak arra, hogy a kvantumelmélet helyes, még ha néha olyan eredményekre is vezet, amit józan paraszti ésszel nehezen tudunk felfogni. Az, hogy tetszőlegesen távoli események között szoros korreláció létezhet információ áramlás nélkül is, nehezen illeszthető bele a makroszkopikus világban tapasztaltakkal. Mindazonáltal pontosan a két világ különbözősége miatt nem tűnik valószínűnek, hogy e “kvantumtapasztalatok” direkt módon befolyásolják makroszkopikus világunkat. Vannak homályos elképzelések arról, hogy a kvantum teleportáció effektusa esetleg használható lesz a technológia bizonyos területein, de ezek a területek sajnálatos módon igen távol esnek a tárgyak továbbításának (szállítás, közlekedés) kérdéskörétől.
Tapasztalataim alapján bátran felhívom laikus természetbúvár társaim figyelmét hasonló szellemi túrák megtételére. Természetesen szükség van bizonyos szintű angol nyelvtudásra és egy megbízható Internet kapcsolatra is (és persze jól jön néha egy szakmabeli ismerős, vagy rokon is).
Első lépésként az Internetet használva könnyen összegyűjthetjük a kiválasztott témakör releváns dokumentumait, értve ezalatt a nem tudományos anyagokat is. Második lépésként megpróbáljuk visszafejteni az anyagok összefüggéseit a források dátuma és hivatkozásai révén. Innen kétfele vezet az út. Megpróbálhatjuk egy kicsit beásni magunkat a tudományos anyagokba. Általában találunk nem szakembereknek szóló, megbízható ismeretterjesztő anyagokat is egy kis figyelmes szelektálással. A másik út annak a felfedezése, hogy hogyan és miért engedjük magunkat oly könnyen becsapni a szenzációhajhász hírek által. Ez utóbbi túra segíteni fog minket beilleszkedni a “megtévesztettek” gondolkozásába, ami elsőrendű fontosságú a hatékony ebéd utáni vita lefolytásához.
Már ha egyáltalán felvesszük a kesztyűt…
Források
 Ez a cikk eredetileg a Természet világa 1999. júliusi (130. évf. 7. sz.) 296-301. oldalán jelent meg.
Ez a cikk eredetileg a Természet világa 1999. júliusi (130. évf. 7. sz.) 296-301. oldalán jelent meg.







